Current Collaborators: A. I. Akinwande (EECS), S. Guerrera (EECS), X. Wang (EECS)
Funding: DARPA/MTO, AFOSR
Mainstream commercial electron sources are based on thermionic emission in which electrons are “boiled” off the surface of metals or semiconductors when the thermal energy of the electrons is sufficient to overcome the potential barrier holding the electrons within the material. Even though thermionic cathode technology is quite successful, thermionic-based cathodes require high-vacuum and high-temperature to operate, which results in inefficient power consumption, poor reliability, and portability constraints. The demand for more efficient electron sources has driven the research of cold cathode technologies, particularly field emission. Field emission arrays (FEAs) are potential cold cathodes that could be used in a variety of vacuum micro- and nano-electronic device applications such as field emission displays (FEDs), high frequency amplifiers, gas ionizers, X-ray sources, and multi-electron beam lithography. In the majority of these applications current level, stability, reliability, lifetime, and emission uniformity are the key metrics for cathode performance.
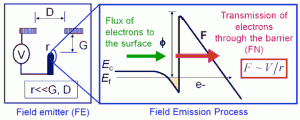
Field emission of electrons from metal or semiconductor surfaces consists of two processes (Fig. 1):
- Transmission of electrons (quantum tunneling) through the potential barrier that holds electrons within the material (workfunction Φ) when the barrier is deformed by the application of a high electrostatic field
- Supply of electrons from the bulk of the material to the emitting surface.
Either the transmission process or the supply process could be the limiting step that determines the emission current of the field emitter (FE). Control of the transmission process to produce high uniform current from FEAs has largely been unsuccessful due to the physics of the field emission process. The Fowler-Nordheim (FN) equation relates the current density to the electrostatic field and the work function. IE(VG), i.e., the current emitted from a tip biased at a voltage VG is
where Atip (cm2) is the emitting area of the tip, Φ (eV) is the workfunction of the tip, Elocal(VG) (V/cm) is the local electrostatic field at the emitter tip, AFN = q3/(8πh) and BFN = (8π/3)/(√(2m)/qh)where q is the electronic charge, h is Plank’s constant, and m is the electron’s mass, and t(y) and v(y) are the Nordheim elliptic functions where y = and εo is the electrical permittivity of free space. The Nordheim elliptic functions can be approximated as t(y)= 1.1 and v(y)=0.95-y2. The local electric field is related to the applied voltage VG through Elocal(VG) = β.VG where β (cm-1) is the field factor. Therefore, Eq. 1 can be rewritten as
The field factor β relates the bias voltage to the surface electrostatic field and it is to first order equal to the inverse of the tip radius r. About 3×107 V/cm are needed to field emit electrons.